Chaos

Lorenz attractor as a prototypical chaotic system (left) and distance between the nearby trajectories (right). The butterfly effect is the popular name for the divergence of nearby trajectories, which is typical of chaotic systems. The largest Lyapunov exponent is the slope of the straight line (right). Project of Francisco Huhn.

Optimization of chaotic thermoacoustic oscillations. Project of Francisco Huhn.

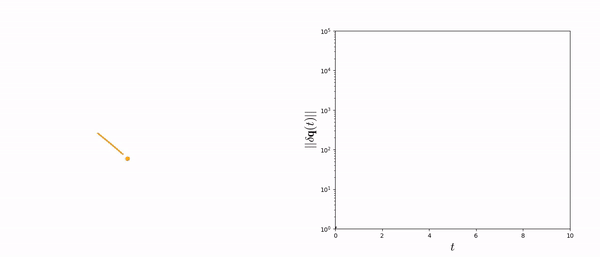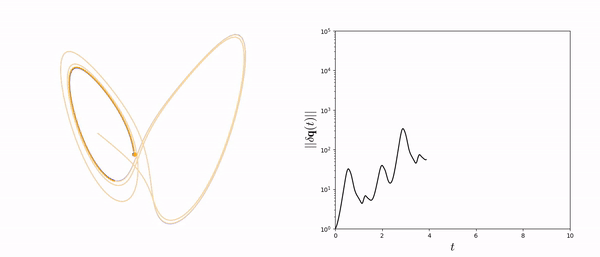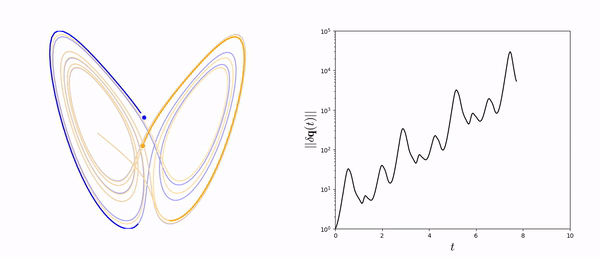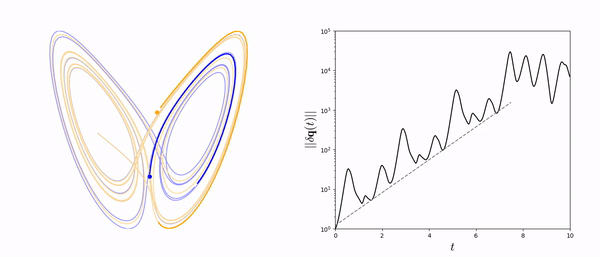
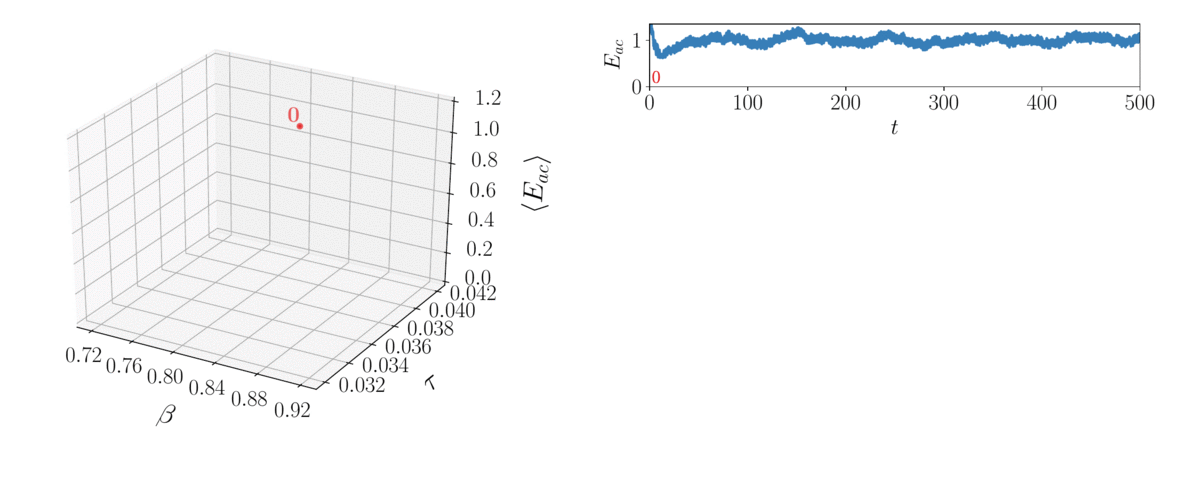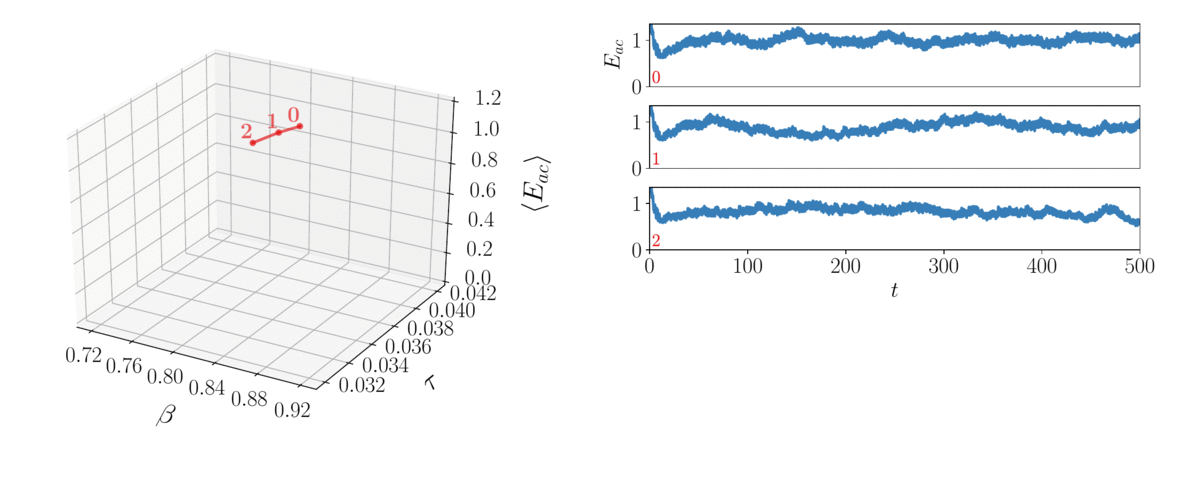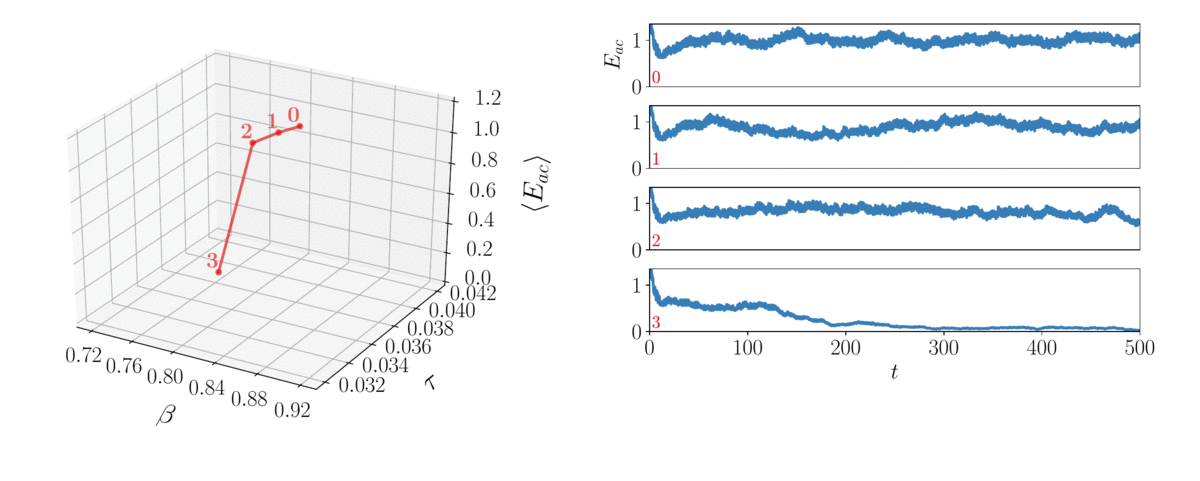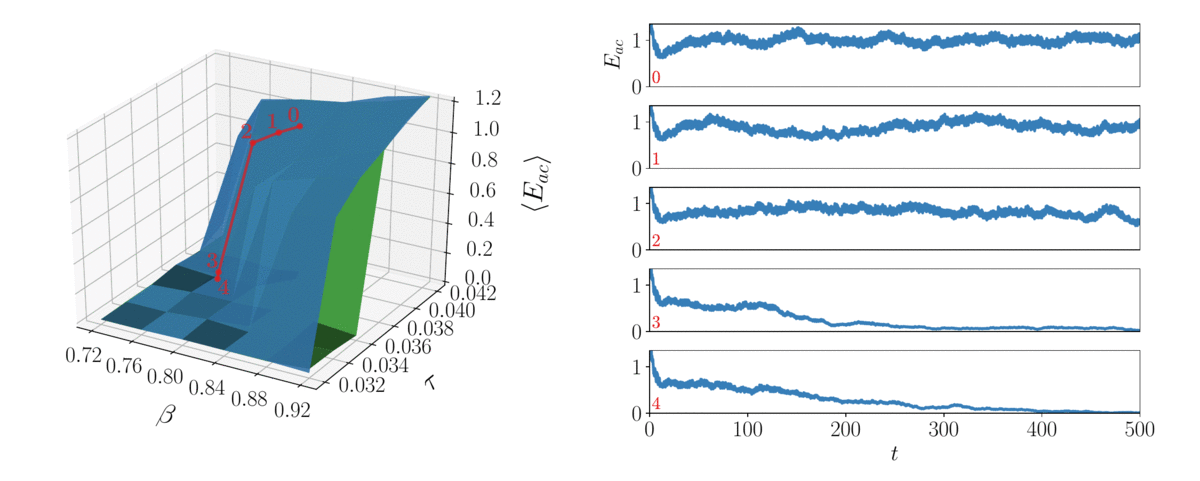
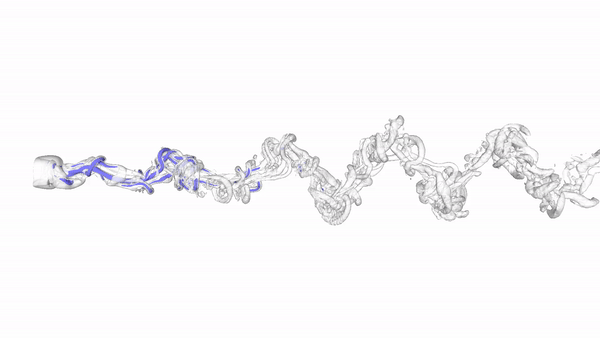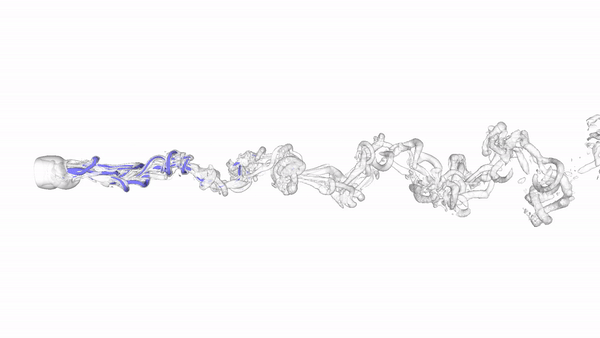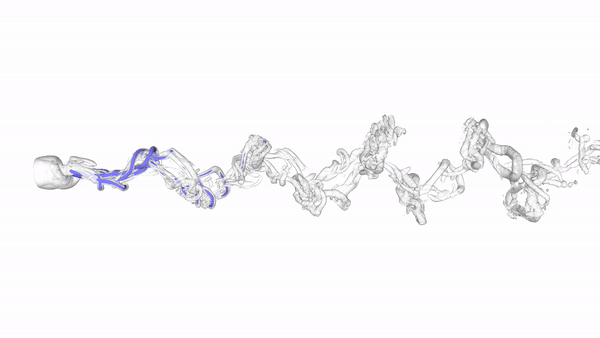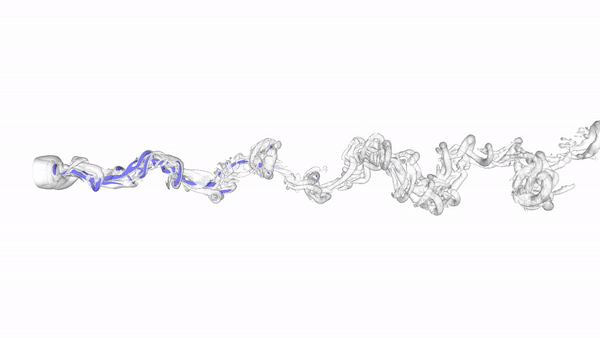
In the time domain, reacting-flow dynamics are typically turbulent, thereby chaotic. Although time-averaged quantities are predictable, any finite-time average, which is the actual output of numerical computations, is less predictable because it differs from its infinite-long time average counterpart by a small amount. Due to the "butterfly effect", a small change in the design can propagate this error, which, in turns, amplifies the uncertainty on the desired infinite-long time average. This makes the design of aeroengines with minimal NOx and noise emissions, and sports cars with minimal air resistance, cumbersome. We combine Lyapunov covariant vector analysis to calculate the stability of chaotic systems, and optimize them with shadowing methods.

Symmetry breaking in wakes

Bifurcations of the wake past a bluff body, direct numerical simulation. Symmetry breaking in a 3D bluff-body wake Rigas, G., Esclapez, L. & Magri, L., Proceedings of the Center for Turbulence Research Summer Program (2016), pp. 193-202.

Direct numerical simulation of the wake past a bluff body.

Dominant covariant Lyapunov vector of the chaotic wake past a bluff body.

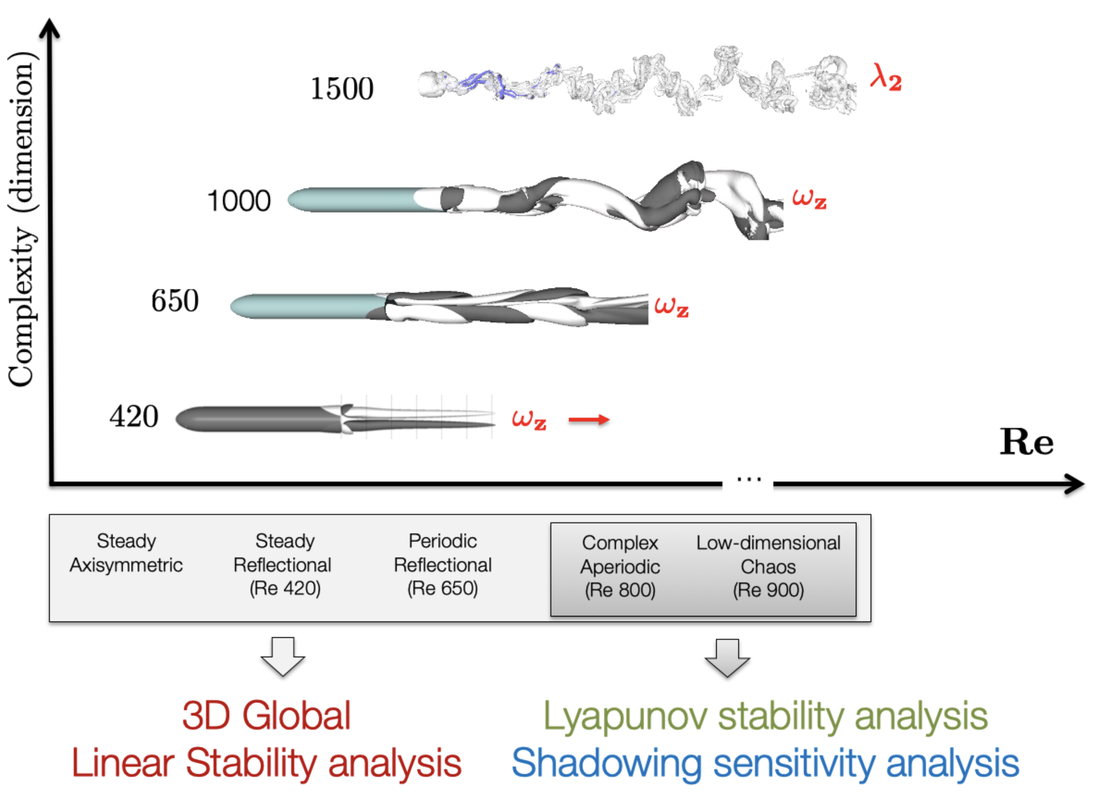
Bluff-body flows are of fundamental importance to many industries, in particular the transport industry, where the aerodynamic drag arising from such flows can be the dominant source of vehicle fuel-burn and CO2 emissions. Recent advances in hydrodynamic stability have further aided understanding and controlling laminar and transitional regimes, particularly in two-dimensional (2D) flows. However, flows of practical and industrial interest involve three-dimensional (3D) wakes and high Reynolds numbers. Despite their turbulence and complexity, such flows exhibit organization, which manifests as coherent structures. These structures are usually associated with increased noise, structural fatigue and drag.
During the transitional regime of laminar wakes, continuous spatial and temporal symmetries are spontaneously broken through a sequence of bifurcations. Specifically, the axisymmetric 3D wake undergoes a steady bifurcation followed by a spiral unsteady bifurcation at low Reynolds numbers prior to the emergence of chaos. These bifurcations break spatial-rotational and time-translation symmetries, giving rise to a reflectionally symmetric steady flow and unsteady vortex shedding, which persist at high Reynolds numbers. Understanding the physics of such non-reacting wakes is important in combustion problems as well, where the flame holder wake dynamics plays an essential role in stabilizing the flame due to the recirculation of hot products.