Super-resolution and reconstruction
What is Super-Resolution and Reconstruction?
We know that physical systems are governed by underlying processes and equations. In real-world scenarios, we can only take a finite number of measurements; for instance, in running an experiment you may only be able to take measurements at a few locations as you have a fixed number of sensors available. Super-resolution is the process of taking a small number of observations and recovering the high-resolution field from which these observations were obtained. A simple example would be the flow around an aeroplane wing: we can measure pressure at discrete locations, but want to gain an understanding of what the full flow field looks like; super-resolution provides the tools for this.
Many approaches to super-resolution rely on having examples of what the high-resolution data should look like. We can exploit this to learn how to recover the high-resolution data from the low-resolution data, a form of inverse problem. Common approaches to this employ a form of machine learning, using a model to parameterise a mapping from low- to high-resolution. These models are trained through an optimization problem which seeks to minimise a loss term. In the classic data-driven setting (where high-resolution samples are available), a measure of error between model predictions, and true, high-resolution samples is minimised.
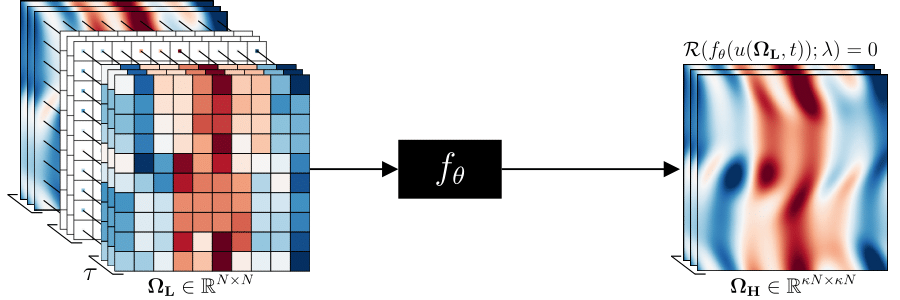
The figure below demonstrates the typical super-resolution task. There exists a physical system from which we are able do draw a finite number of observations from (left); we use a model-based parameterisation to learn a mapping from the low- to high-resolution (right).
The figure below demonstrates the typical super-resolution task. There exists a physical system from which we are able do draw a finite number of observations from (left); we use a model-based parameterisation to learn a mapping from the low- to high-resolution (right).
In many real-world scenarios, we do not have access to high-resolution examples - in particular for experimental data. We do, however, have prior knowledge of the physical equations which govern the systems from which the data was observed. Our group's research focuses on how we can incorporate prior knowledge of the underlying physics to enable improved super-resolution results, or for super-resolution in the absence of high-resolution labels; a problem of fundamental importance in the physical sciences.
An example of practical application:
Super-resolving turbulence
Super-resolving turbulence
In our recent work, we explore the application of physics-constrained convolutional neural networks for flow-field super-resolution in the absence of high-resolution labels. In this work we consider data generated through solution of forced, two-dimensional, turbulent-chaotic turbulence in a periodic domain; known as the Kolmogorov flow. We seek the solution of an inverse problem, namely; recovering the high-resolution flow-field given low-resolution spatial observations on a fixed grid. Our model-based parameterisation for the super-resolution task is based on a convolutional neural network, an architecture which exploits spatial correlations, key to the super-resolution task.
Our work focuses on proposing and demonstrating the application of a new training mechanism which exploits knowledge of the underlying partial differential equation from which the data is generated. Namely, we observe that the Kolmogorov flow satisfies the incompressible Navier-Stokes equations, with periodic boundary conditions. We pose the super-resolution task as an optimisation problem, seeking to minimise a combination of two loss terms: (i) a data-driven loss term which ensures that the recovered high-resolution field is self-consistent with the given low-resolution field; and (ii) a physics-constrained loss term which seeks to minimise the residual of the momentum equation.
In order to compute the residual of predictions, we operate on contiguous time-steps, allowing us to compute the time-derivative explicitly. The differential operator in the momentum equation is evaluated using a differentiable, pseudo spectral solver (https://github.com/magrilab/kolsol), this has two distinct benefits: (i) we can backpropgate through the loss evaluation in order to compute the sensitivity of the loss with respect to the weights which parameterise the network; and (ii) we are able to evaluate spatial derivative with spectral accuracy, avoiding numerical errors introduced through using a finite-difference-based approach.
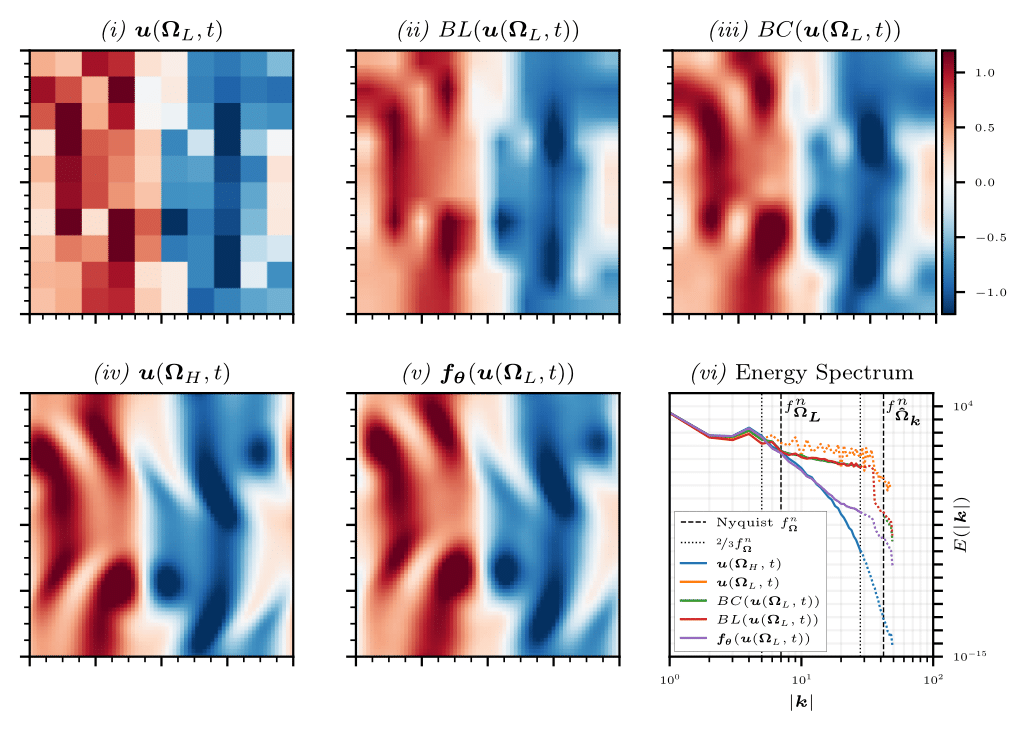
Results in the figure below demonstrate the ability to recover the high-resolution field from a low-resolution input. Data is generated on a 70x70 grid, before being downsampled to 10x10; these are demonstrated in panels (iv, i) respectively. Training the network in absence of high-resolution labels yields a high-resolution flow-field depicted in panel (v). This prediction is compared with naive upsampling methods: bi-linear interpolation, panel (ii); and bi-cubic interpolation, panel (iii). While this is a demonstration for a single snapshot, we conduct super-resolution across the entire time-domain for each method and compare the resulting energy spectrums, as shown in panel (vi). We observe that the physics-constrained approach accurately recovers the turbulent kinetic energy spectrum up to an absolute wavenumber of around 18, constituting over 99% of the energy in the system.
Our work focuses on proposing and demonstrating the application of a new training mechanism which exploits knowledge of the underlying partial differential equation from which the data is generated. Namely, we observe that the Kolmogorov flow satisfies the incompressible Navier-Stokes equations, with periodic boundary conditions. We pose the super-resolution task as an optimisation problem, seeking to minimise a combination of two loss terms: (i) a data-driven loss term which ensures that the recovered high-resolution field is self-consistent with the given low-resolution field; and (ii) a physics-constrained loss term which seeks to minimise the residual of the momentum equation.
In order to compute the residual of predictions, we operate on contiguous time-steps, allowing us to compute the time-derivative explicitly. The differential operator in the momentum equation is evaluated using a differentiable, pseudo spectral solver (https://github.com/magrilab/kolsol), this has two distinct benefits: (i) we can backpropgate through the loss evaluation in order to compute the sensitivity of the loss with respect to the weights which parameterise the network; and (ii) we are able to evaluate spatial derivative with spectral accuracy, avoiding numerical errors introduced through using a finite-difference-based approach.
Results in the figure below demonstrate the ability to recover the high-resolution field from a low-resolution input. Data is generated on a 70x70 grid, before being downsampled to 10x10; these are demonstrated in panels (iv, i) respectively. Training the network in absence of high-resolution labels yields a high-resolution flow-field depicted in panel (v). This prediction is compared with naive upsampling methods: bi-linear interpolation, panel (ii); and bi-cubic interpolation, panel (iii). While this is a demonstration for a single snapshot, we conduct super-resolution across the entire time-domain for each method and compare the resulting energy spectrums, as shown in panel (vi). We observe that the physics-constrained approach accurately recovers the turbulent kinetic energy spectrum up to an absolute wavenumber of around 18, constituting over 99% of the energy in the system.
We note that training was conducted on just 2048 samples, constituting less than 2% of the simulated time-domain. The convergence of the predicted energy spectrum to the true energy spectrum speaks to the generalisation capabilities of the method.
Material, activities, and people
This work was part of Super-resolving sparse observations in partial differential equations: A physics-constrained convolutional neural network approach, D. Kelshaw, L.Magri (2023). All code is available at https://github.com/magrilab/pisr
D. Kelshaw. and L. Magri. acknowledge support from the UK Engineering and Physical Sciences Research Council. L. Magri gratefully acknowledges financial support from the ERC Starting Grant PhyCo 949388.
Article written by Daniel Kelshaw and Luca Magri.
D. Kelshaw. and L. Magri. acknowledge support from the UK Engineering and Physical Sciences Research Council. L. Magri gratefully acknowledges financial support from the ERC Starting Grant PhyCo 949388.
Article written by Daniel Kelshaw and Luca Magri.
An example of practical application:
Predicting chaos from partial data
Predicting chaos from partial data
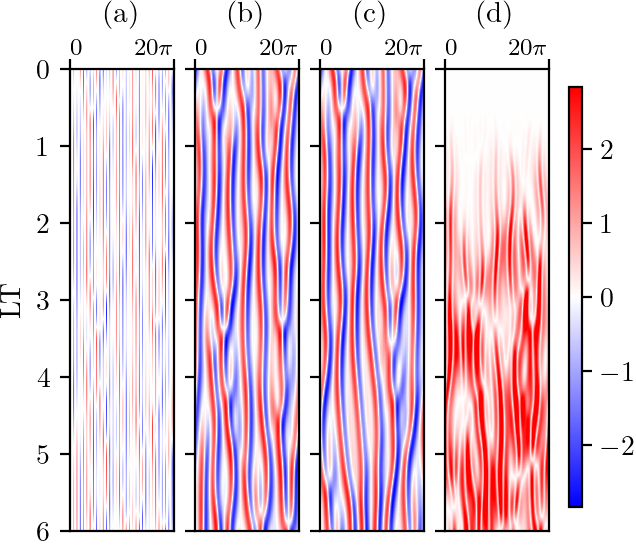 Comparison of a test data set’s (a) input, (b) label/reference solution, (c) LH-LSTM’s closed-loop
prediction, and (d) the absolute error between the target and LH-LSTM prediction.
Comparison of a test data set’s (a) input, (b) label/reference solution, (c) LH-LSTM’s closed-loop
prediction, and (d) the absolute error between the target and LH-LSTM prediction.
One application of employing machine learning for super-resolution can be found in super-resolving partial differential equations. Once trained, neural networks provide computationally cheap predictions and can be applied to noisy, undersampled observations.
Specifically, one idea is to infer the high-resolution dynamics from low-resolution inputs, thereby reducing the cost of acquiring full measurement data. Especially in fluid dynamics, in which problems display turbulent behavior, this task becomes especially difficult as the prediction is sensitive due to the chaotic nature of the data. When sequential data is available, a recurrent neural network, such as a long short-term memory (LSTM), can be used for reconstruction and prediction.
To demonstrate how well LSTMs can infer the full-state dynamics from partial data, especially in capturing small-scale statistics in partial-differential equations, we train the network on partial observations of the Kuramoto-Sivashinsky equation. The Kuramoto-Sivashinsky equation is a 1D partial differential equation that exhibits chaotic behavior. The spatial domain is discretized into 128 degrees of freedom, of which only 32 are selected as training input to the LSTM. The loss function of the LSTM is then constructed as the mean-squared error between the partial input and the full label. Therefore, the LSTM produces a high-resolution prediction from low-resolution data, and we refer to it as LH-LSTM. After training the network, we observe that it successfully reconstructs the missing degrees of freedom to high accuracy in the test set. Further, the LSTM autonomously predicts the high-resolution data for multiple time steps without any reference data.
This demonstrates the potential that machine learning algorithms have in the extrapolation of physical behavior from limited data.
Specifically, one idea is to infer the high-resolution dynamics from low-resolution inputs, thereby reducing the cost of acquiring full measurement data. Especially in fluid dynamics, in which problems display turbulent behavior, this task becomes especially difficult as the prediction is sensitive due to the chaotic nature of the data. When sequential data is available, a recurrent neural network, such as a long short-term memory (LSTM), can be used for reconstruction and prediction.
To demonstrate how well LSTMs can infer the full-state dynamics from partial data, especially in capturing small-scale statistics in partial-differential equations, we train the network on partial observations of the Kuramoto-Sivashinsky equation. The Kuramoto-Sivashinsky equation is a 1D partial differential equation that exhibits chaotic behavior. The spatial domain is discretized into 128 degrees of freedom, of which only 32 are selected as training input to the LSTM. The loss function of the LSTM is then constructed as the mean-squared error between the partial input and the full label. Therefore, the LSTM produces a high-resolution prediction from low-resolution data, and we refer to it as LH-LSTM. After training the network, we observe that it successfully reconstructs the missing degrees of freedom to high accuracy in the test set. Further, the LSTM autonomously predicts the high-resolution data for multiple time steps without any reference data.
This demonstrates the potential that machine learning algorithms have in the extrapolation of physical behavior from limited data.
Material, activities, and people
This work was part of
Reconstruction, forecasting, and stability of chaotic dynamics from partial data , E.Özalp, G.Margazoglou and L.Magri, Chaos (2023).
This research has received financial support from the ERC Starting Grant No. PhyCo 949388.
Link to code repository, add references with links, names, and sponsors. At the end of this webpage/paragraph "Article written by Elise Özalp and Luca Magri."
Reconstruction, forecasting, and stability of chaotic dynamics from partial data , E.Özalp, G.Margazoglou and L.Magri, Chaos (2023).
This research has received financial support from the ERC Starting Grant No. PhyCo 949388.
Link to code repository, add references with links, names, and sponsors. At the end of this webpage/paragraph "Article written by Elise Özalp and Luca Magri."