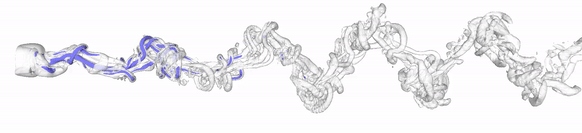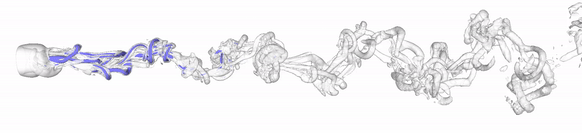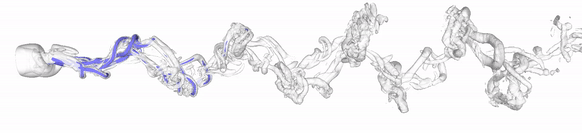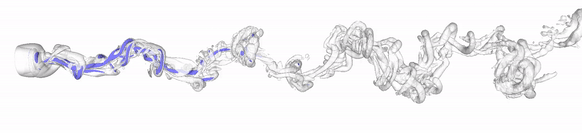
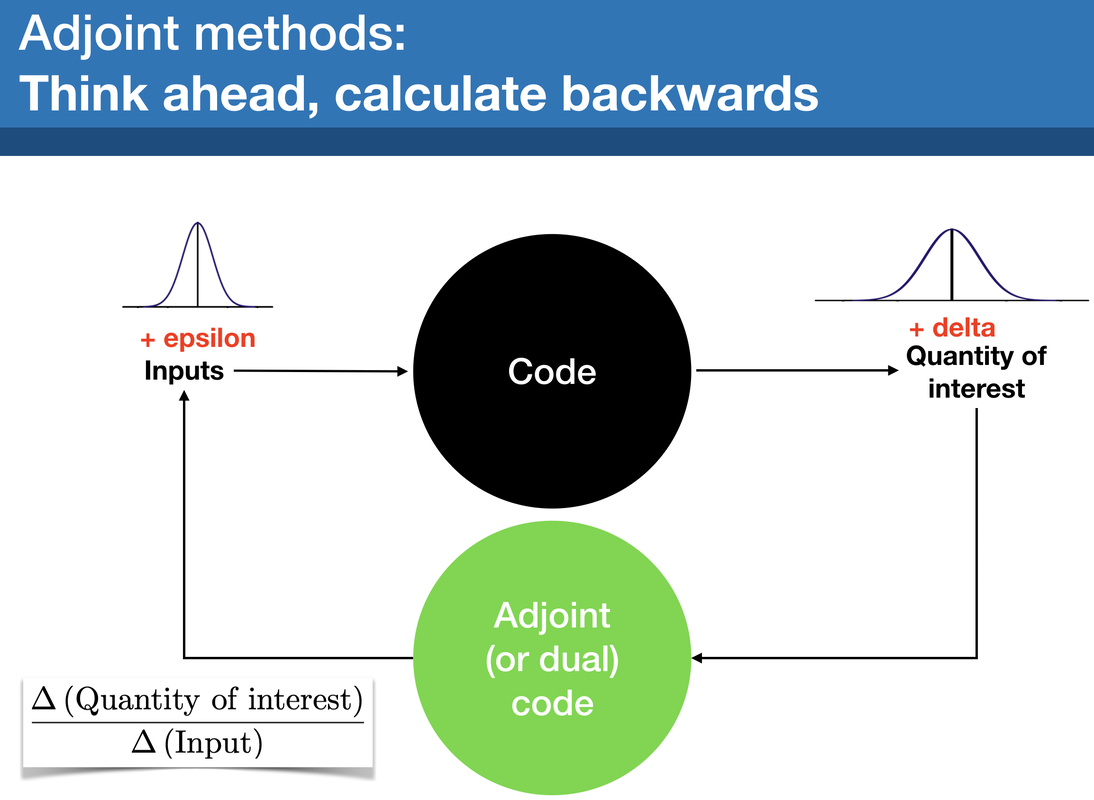
Overview

The three big Us are (some of) the reasons for which it is difficult to time accurately predict the evolution of unsteady thermo-fluid dynamics. Example of a wake past a bluff body.

The chaotic nature of many flows, such as turbulent flows, makes the time-accurate prediction of the dynamics very difficult. This is because after a time horizon, which scales with the inverse of the Lyapunov exponent, a little perturbation to the flow equations is exponentially amplified in time. The perturbation can be caused by floating-point arithmetic, numerical schemes, number of processors, parallelization of the code, initial conditions, boundary conditions, parameters, etc.

It is important to understand human learning before doing machine learning!

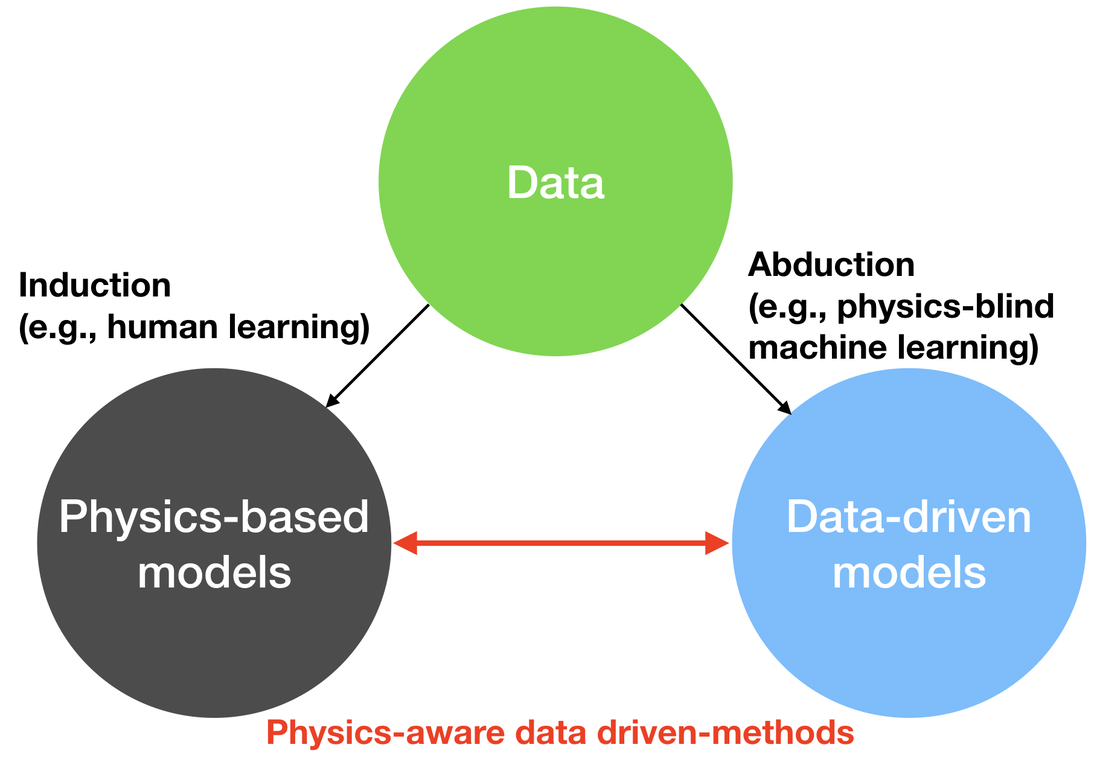
1. Reduced-order models are practical tools but they have parameter/model uncertainties. 2. High-fidelity simulations are accurate tools but they cannot time-accurately capture rare/extreme events. 3. Data driven methods help combine data with models but we ought not to forget the physical constraints.

Adjoint methods enable the fast and accurate calculation of the sensitivity of a cost functional when the design parameters are many. We use adjoint methods for stability calculations, data assimilation, uncertainty quantification, multiple-scale methods, optimization, and other applications.