Chaotic time series forecasting
Precisely, it is given by
where x(t) is the state of a physical system over time t and F(·) is referred to as dynamics.To address the complexity in prediction, machine learning methods have been integrated into the forecasting process. Recurrent Neural Networks (RNNs) are a class of artificial neural networks designed to process sequential data, making them well-suited for time series modeling and forecasting. They have the capacity to capture complex temporal dependencies and patterns. By training the network on available data, they learn the underlying dynamics of the system, enabling them to make predictions about future states. By combining chaotic systems understanding and machine learning, we can gain insight into complex dynamics from experiments and observations, and predict future states when traditional methods fail.
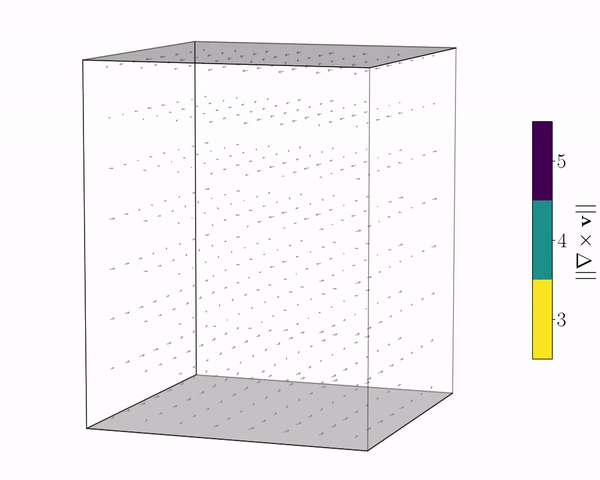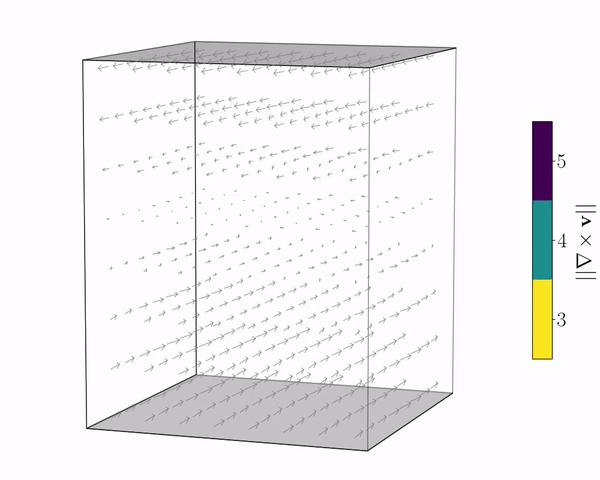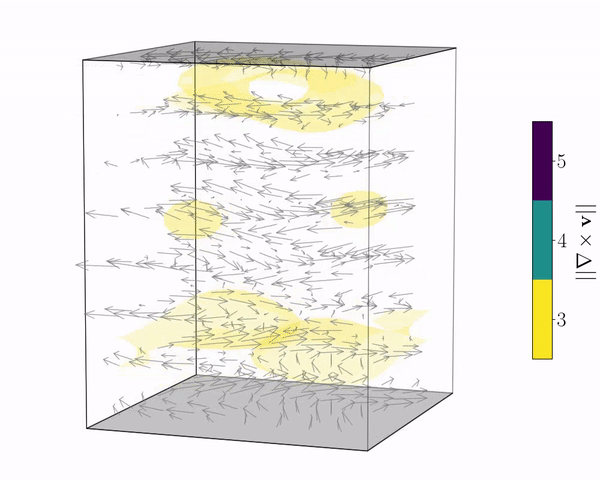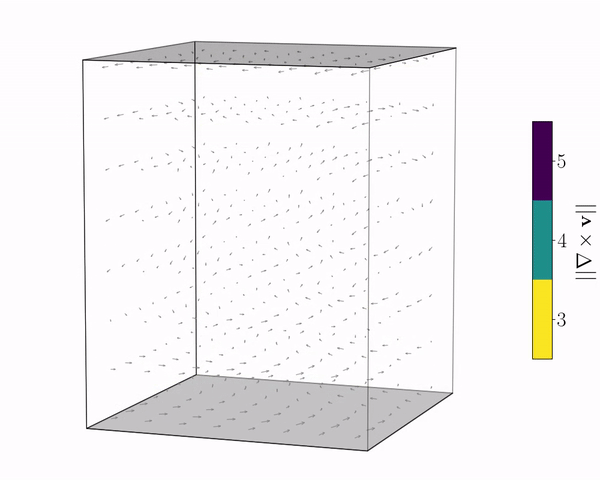
Extreme events are sudden large-amplitude changes in the state or observables, which have typically negative consequences on the system of interest. The events appear in many nonlinear scientific phenomena, such as rogue waves, weather patterns and power grid shocks. Here, we focus on extreme events in a chaotic (turbulent) fluid mechanics, which characterise multiple systems of engineering interest.
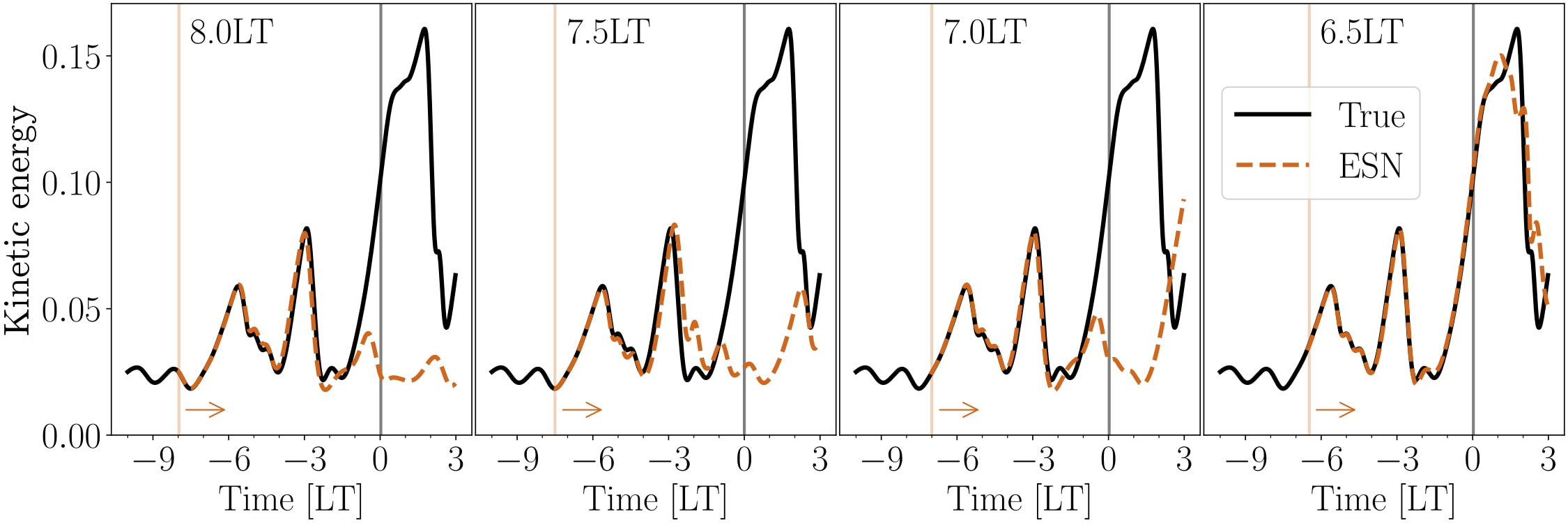
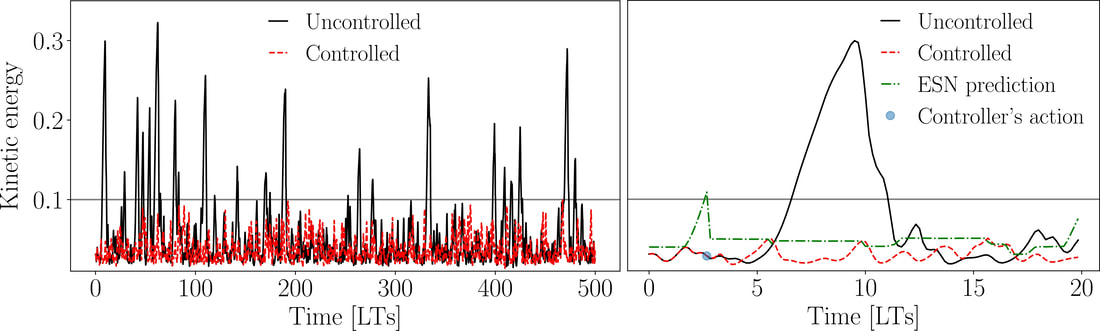
To predict the extreme events, we use echo state networks (ESNs). The ESNs are recurrent neural networks, which are trained on past time series data to predict the future of the system given current measurements. In doing so, they are able to tell us at current time whether an event is happening in the near future. Based on the prediction of the event, we can act on the system in advance to prevent the event from happening, mitigating the negative impacts of the events on the system.
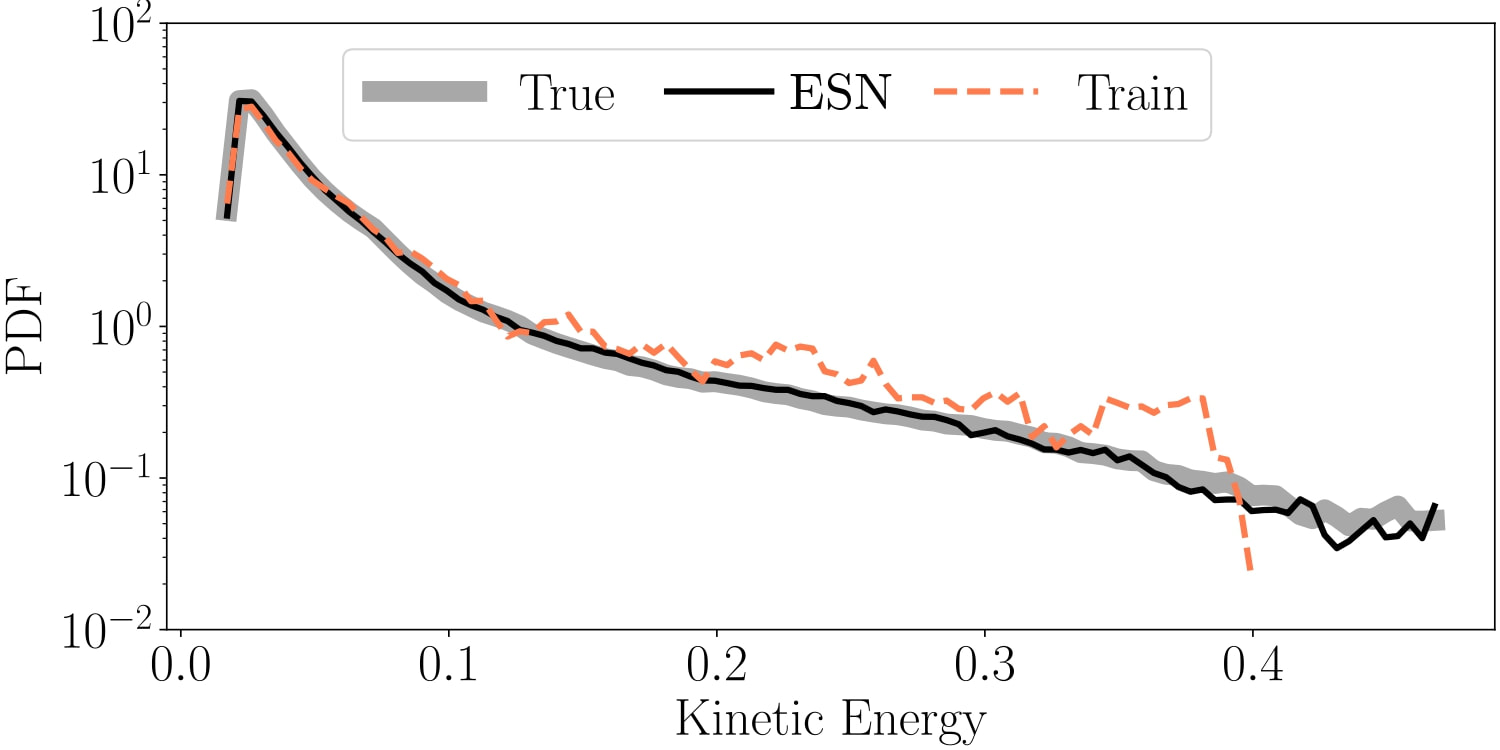
In addition to short-term predictions, we study extreme events also in a statistically sense. By analysing the statistics, we are able to compute the probability of an event happening at any given time. The problem with analysing the statistics of extreme events is that the events are also typically rare, which means that we usually do not have enough data to accurately estimate their probability.
In this scenario, we make long-term predictions with ESNs to extrapolate the statistics and improve the statistical knowledge of the system with respect to the available data for training.
Material
This work was part of the PhD of Alberto Racca. It is published in
Data-driven prediction and control of extreme events in a chaotic flow, A.Racca and L.Magri, PRF (2022).
The code used for this project is publicly available on GitHub.
Research funded by EPSRC, Cambridge Trust and ERC grants.
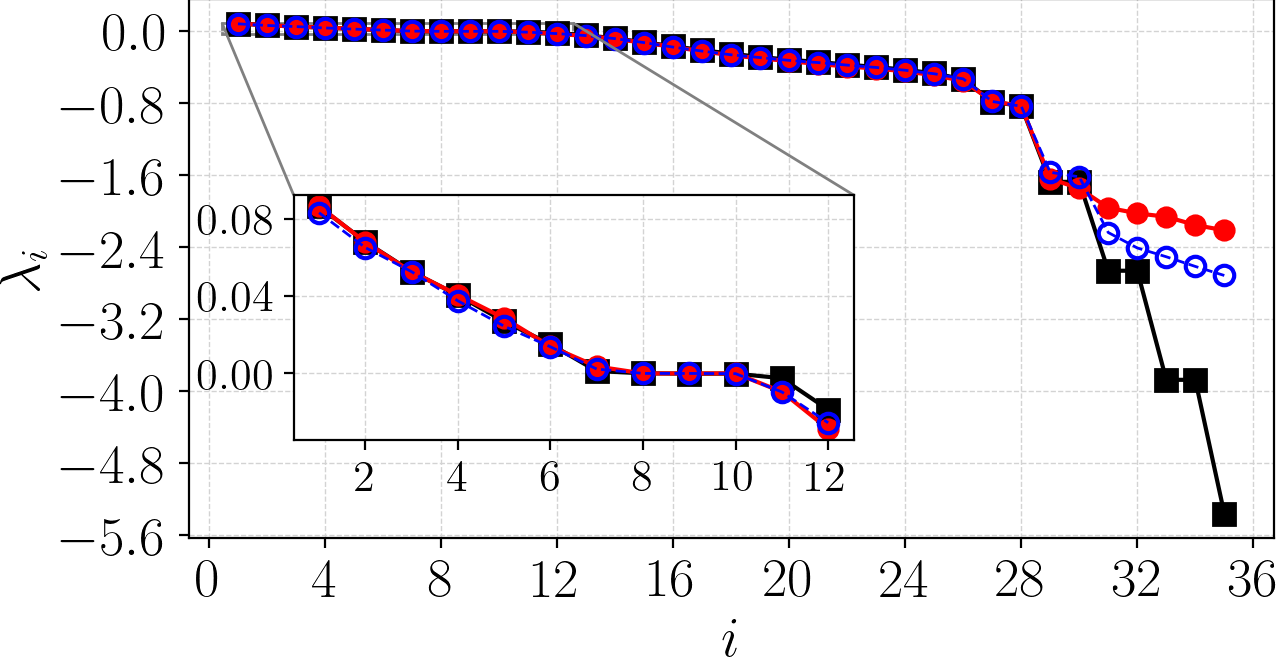
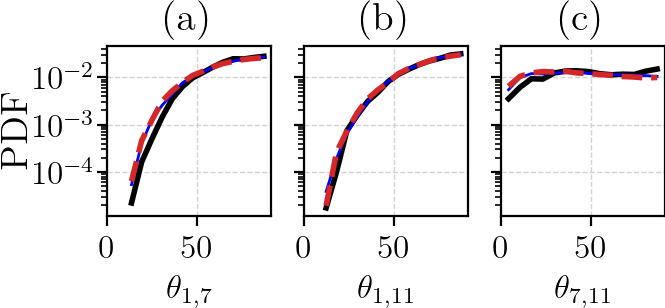
The predictability and stability of a chaotic system are characterized by its tangent space, which can be computed using the linearized dynamics provided by the Jacobian. This computation allows for the derivation of quantities such as the Lyapunov exponents (LEs), which measure the exponential rate of separation of trajectories. A geometric characterization is provided by the covariant Lyapunov vectors (CLVs), which constitute a covariant basis of the tangent space, and point to directions of asymptotic expansion and contraction of the dynamical system.
Preserving these stability properties is crucial when building surrogate models from limited observations to a more comprehensive dataset.
To ensure the physical consistency of ML surrogate models with the underlying dynamics, we can assess the model's stability properties. This evaluation holds profound implications for the explainability and interpretability of neural networks, when the stability properties of the original system are reproduced.
We have successfully demonstrated that the LSTM reproduces the stability properties of multiple chaotic systems, such as the Kuramoto-Sivashinsky equation, even when trained on partial data.
Reconstruction, forecasting, and stability of chaotic dynamics from partial data , E.Özalp, G.Margazoglou and L.Magri, Chaos (2023).
This research has received financial support from the ERC Starting Grant No. PhyCo 949388.
Article written by Elise Özalp, Alberto Racca and Luca Magri.