Optimization

Multiple-scale methods.

Adjoint methods greatly speed up the uncertainty quantification of stability calculations. Example of an annular combustor.

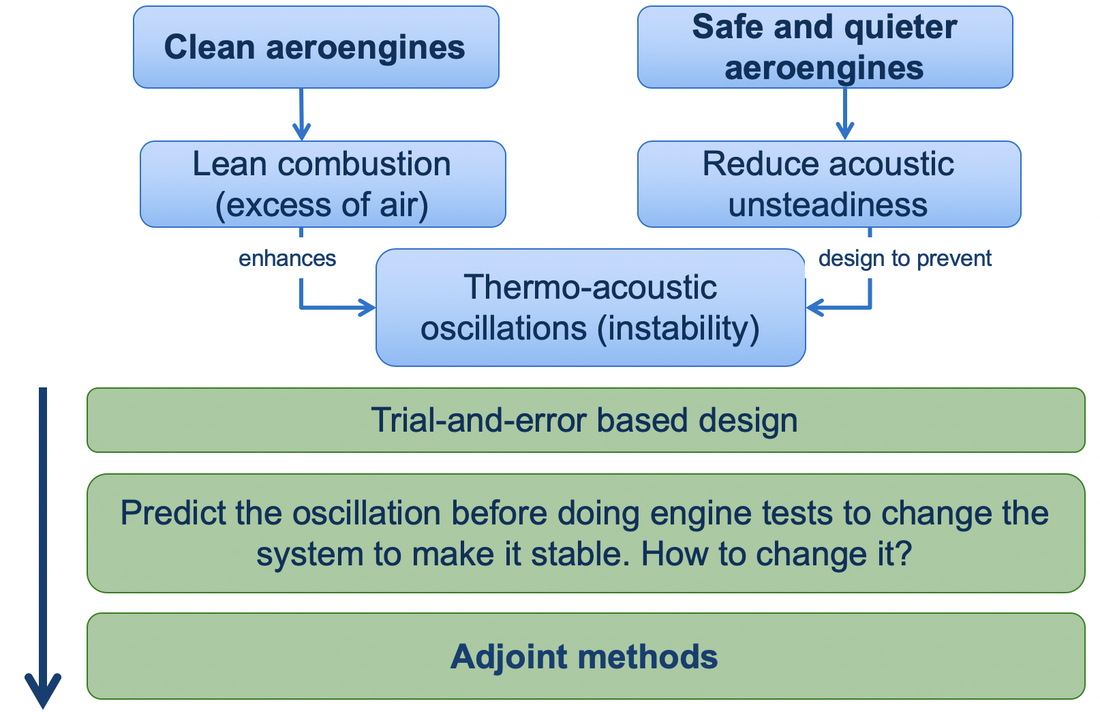
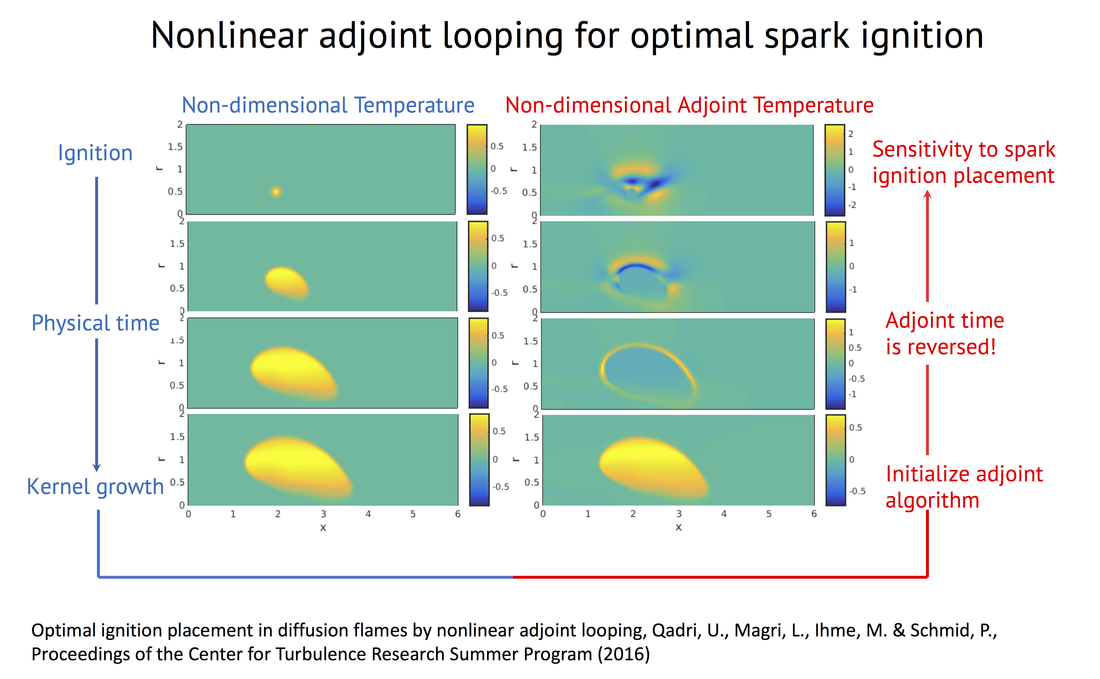
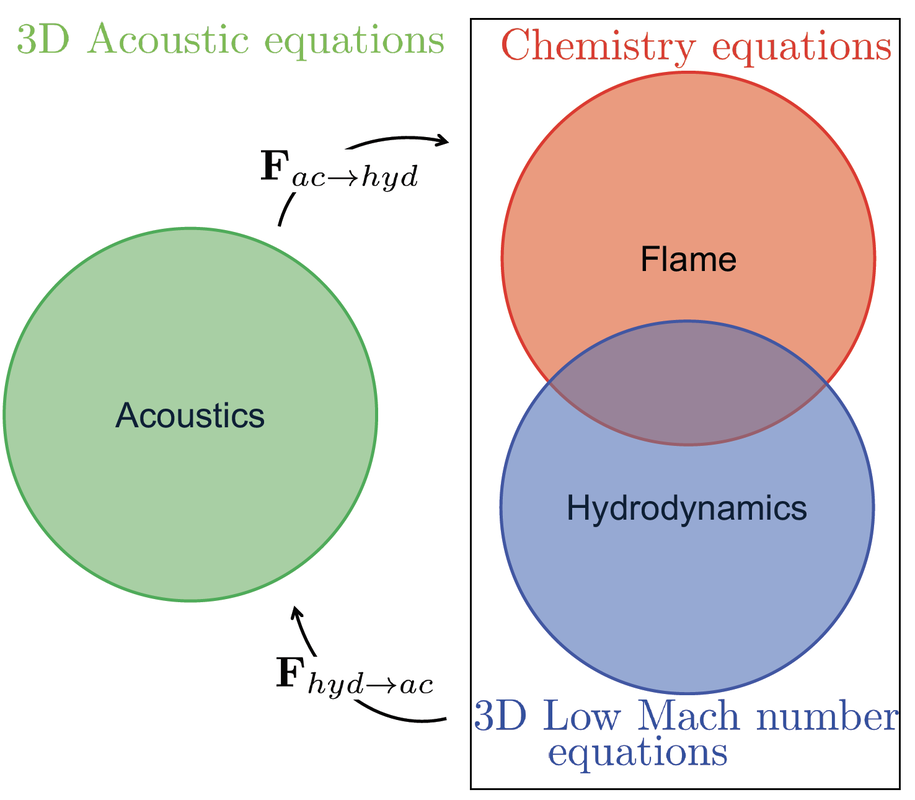
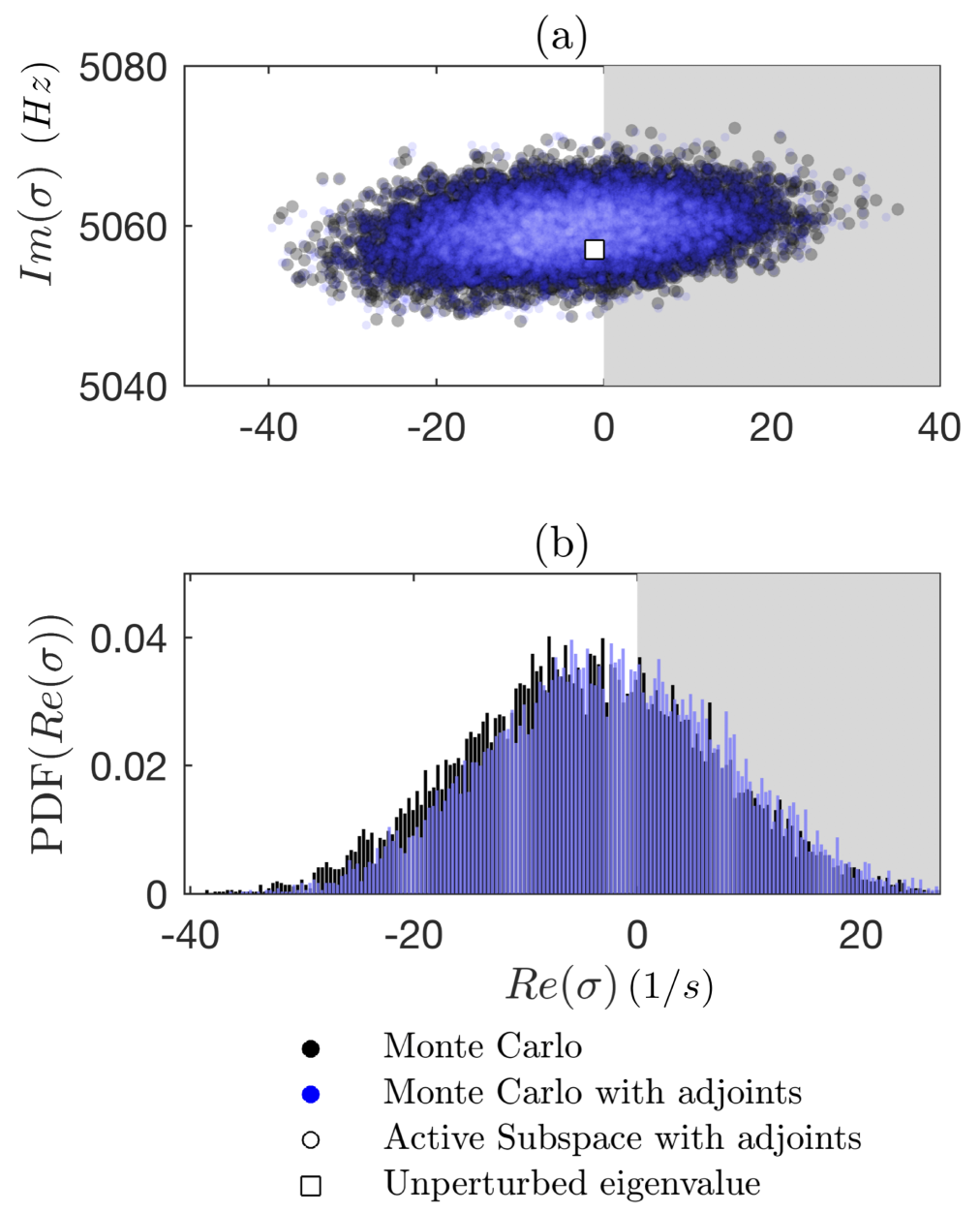
In the frequency-domain analysis, the eigenvalue is one of the most important quantities because it informs about the (linear) stability of the system. Combustion systems are characterized by many parameters, however, in situations that are susceptible to combustion oscillations, often only a handful of oscillation modes are unstable. Existing techniques examine how a change in one parameter affects all (calculated) oscillation modes, whether unstable or not. Adjoint techniques turn this around. In a single calculation, they examine how each oscillation mode is affected by changes in all parameters. In other words, they provide gradient information about the variation of an eigenvalue with respect to all the parameters in the model. In a system with a million parameters, they calculate gradients a million times faster than finite difference methods. The sensitivity information from the adjoint calculation can also be exploited to calculate, among all possible positions,  the optimal position where to place an external passive device to control an instability.