Physics-aware machine learning
What is physics-aware machine learning?
Physical systems are traditionally modelled based on first principles. For example, in classical mechanics, Newton’s second law describes the motion of an object when a force acts on it. These equations provide valuable physical knowledge, however high-fidelity models can be time consuming to solve. Low-fidelity models, on the other hand, are simplified. Data-driven methods have emerged as computationally cheaper alternatives, which are also flexible. Recent advances in machine learning have enabled modelling, reconstruction, and forecasting of physical systems from data. These models do not suffer from simplifying assumptions and with more data, one can capture more complexities of the underlying systems. The downside of these models is that they are often black-box models that are hard to interpret. Furthermore, the acquired data may also be corrupted with noise or may be expensive to obtain, hence scarce. In these cases, we can leverage the vast knowledge of the domain-specific physics. Physics-aware machine learning bridges the gap between first-principles-based approaches and data-driven approaches. By incorporating physics-information, machine learning models are encouraged towards solutions that are also physically meaningful and robust to uncertainties in the data.
What is physics-aware machine learning, a bit more technically?
Constraining prior knowledge into machine learning methods can significantly improve prediction, robustness, and generalizability.
On the one hand, constraints that are imposed in the loss function as penalty terms, which act during training, are referred to as “soft constraints". Soft constraints can include the governing differential equations derived from conservation laws, initial and boundary conditions.
On the other hand, constraints that are imposed in the architecture (as opposed to the training) are referred to as “hard constraints". Hard constraints span the areas of the function space in which physical solutions live, i.e., they create an inductive bias.
On the one hand, constraints that are imposed in the loss function as penalty terms, which act during training, are referred to as “soft constraints". Soft constraints can include the governing differential equations derived from conservation laws, initial and boundary conditions.
On the other hand, constraints that are imposed in the architecture (as opposed to the training) are referred to as “hard constraints". Hard constraints span the areas of the function space in which physical solutions live, i.e., they create an inductive bias.
An example of practical application:
Digital twins of acoustics and thermoacoustics
Digital twins of acoustics and thermoacoustics
Solutions from acoustics and thermoacoustics originate from nonlinear wave equations. Thermoacoustic systems contain nonlinearities in the heat release model, which, when coupled with the acoustics in a positive feedback loop, can generate self-excited oscillations and rich nonlinear behaviours via bifurcations. Because these oscillations can have detrimental effects on the system’s structure and performance, their prediction and control are active areas of research, for example, in gas turbines, and rocket engines. The data typically comes from laboratory experiments that are conducted with setups consisting of a duct with a heat source, which can be a flame or an electrically heated wire mesh. In the experiments, the collected data is usually the acoustic pressure measured by microphones at high sampling rates.
First, given time series data from a time window, our task is to obtain a model that can extrapolate periodic, quasi-periodic, or chaotic behaviour. In experiments, full-state observations may be unavailable or prohibitively expensive, e.g., in acoustics, only pressure data may be available through measurements with microphones. Second, our task is to reconstruct the flow variables over the entire spatial domain from full- or partial noisy state observations, which poses a challenge for purely data-driven models. Third, we seek a robust, generalizable, low-order model for acoustic and thermoacoustic solutions using as little data as possible.
First, given time series data from a time window, our task is to obtain a model that can extrapolate periodic, quasi-periodic, or chaotic behaviour. In experiments, full-state observations may be unavailable or prohibitively expensive, e.g., in acoustics, only pressure data may be available through measurements with microphones. Second, our task is to reconstruct the flow variables over the entire spatial domain from full- or partial noisy state observations, which poses a challenge for purely data-driven models. Third, we seek a robust, generalizable, low-order model for acoustic and thermoacoustic solutions using as little data as possible.
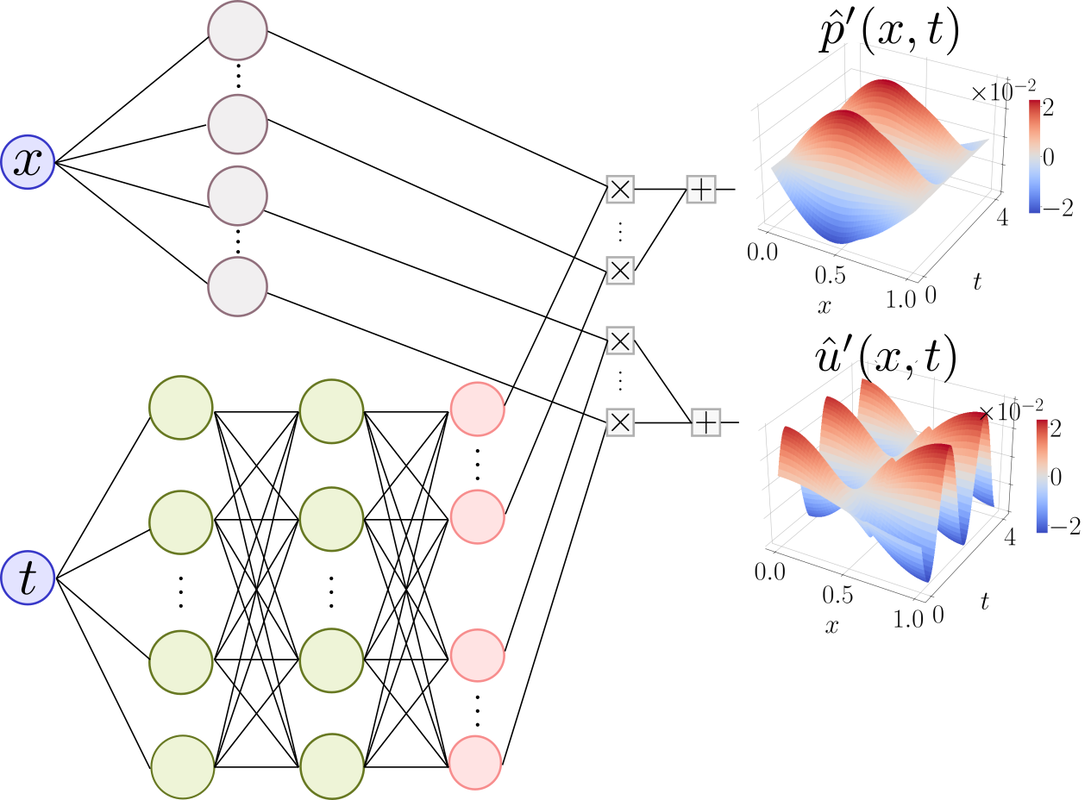
We propose acoustic neural networks that embed the prior knowledge through the activation functions, through a penalization loss function in the training (soft constraint), and through the architecture (hard constraint). We motivate employing periodic activation functions in the standard feedforward neural networks for acoustic problems, the eigenfunctions of which are periodic. Further, we include a physics-based regularization term that penalizes solutions that violate the conservation laws governing the acoustic dynamics. Finally, inspired by Galerkin decomposition, we design a neural network architecture that spans the Hilbert space with the acoustic eigenfunctions as the Galerkin modes, whilst having trainable parameters for inference and closure of the unknown physical terms.
First, we show that standard feedforward neural networks fail at extrapolation, while periodically activated networks can extrapolate and reconstruct accurately from partial measurements. Second, we show the generalizability and robustness of the Galerkin neural networks to higher-fidelity data, which can be noisy and contain only pressure measurements. Hard-constraining neural networks with prior knowledge reduces the required network size, search space of hyperparameters as well as the amount of data required for training.
First, we show that standard feedforward neural networks fail at extrapolation, while periodically activated networks can extrapolate and reconstruct accurately from partial measurements. Second, we show the generalizability and robustness of the Galerkin neural networks to higher-fidelity data, which can be noisy and contain only pressure measurements. Hard-constraining neural networks with prior knowledge reduces the required network size, search space of hyperparameters as well as the amount of data required for training.
Material, activities, and people
This work was part of Hard-constrained neural networks for modelling nonlinear acoustics, D.E. Ozan and L. Magri (2023). preprint.
The code used for this project is publicly available on GitHub.
This research has received financial support from the ERC Starting Grant No. PhyCo 949388.
Article written by Defne Ozan and Luca Magri.
The code used for this project is publicly available on GitHub.
This research has received financial support from the ERC Starting Grant No. PhyCo 949388.
Article written by Defne Ozan and Luca Magri.